Solution. To check whether matrix $\boldsymbol{A}$ is orthogonal, use the definition directly:

Since $\boldsymbol{A}^T\boldsymbol{A}=\boldsymbol{I}_2$, we have that $\boldsymbol{A}$ is an orthogonal matrix.

Proof. By definition of orthogonal matrices, we have that:

By definitionlink of matrix inverses, if the product of any matrix $\boldsymbol{A}$ and $\boldsymbol{B}$ results in the identity matrix, then $\boldsymbol{A}$ is an inverse of $\boldsymbol{B}$ and vice versa. In this case then, we have that $\boldsymbol{Q}^T$ must be the inverse of $\boldsymbol{Q}$. This completes the proof.

Proof. If $\boldsymbol{Q}$ is an orthogonal matrix, then $\boldsymbol{Q}^{-1}=\boldsymbol{Q}^T$ by propertylink. Since the transpose of a matrix always exists, $\boldsymbol{Q}^{-1}$ always exists. This means that $\boldsymbol{Q}$ is invertible by definitionlink. This completes the proof.

Proof. Because $\boldsymbol{Q}^T=\boldsymbol{Q}^{-1}$, we have that:

This completes the proof.

Proof. We first prove the forward proposition. Assume matrix $\boldsymbol{Q}$ is orthogonal. We know from the previous theoremlink that:

Now, taking the transpose of a matrix twice results in the matrix itself, that is:

Substitute this expression for $\boldsymbol{Q}$ into $\boldsymbol{Q}\boldsymbol{Q}^T$ in \eqref{eq:mRczyO42IwvNUv4Luv9} to get:

Here, $(\boldsymbol{Q}^T)^T$ is the transpose of $\boldsymbol{Q}^T$, and their product results in the identity matrix. This means that $\boldsymbol{Q}^T$ must be orthogonal by definition.

We now prove the converse. Assume $\boldsymbol{Q}^T$ is an orthogonal matrix. We have just proven that taking a transpose of an orthogonal matrix results in an orthogonal matrix. The transpose of $\boldsymbol{Q}^T$ is $\boldsymbol{Q}$, which means that $\boldsymbol{Q}$ is orthogonal.

This completes the proof.

Proof. We first prove the forward proposition. We assume matrix $\boldsymbol{Q}$ is orthogonal. By theoremlink, if $\boldsymbol{Q}$ is orthogonal, then $\boldsymbol{Q}^T$ is orthogonal. Because $\boldsymbol{Q}^T=\boldsymbol{Q}^{-1}$ by theoremlink, we have that $\boldsymbol{Q}^{-1}$ is orthogonal.

We now prove the converse. Assume $\boldsymbol{Q}^{-1}$ is orthogonal. We have just proven that taking the inverse of an orthogonal matrix results in an orthogonal matrix. The inverse of $\boldsymbol{Q}^{-1}$ is $\boldsymbol{Q}$ by theoremlink, which means that $\boldsymbol{Q}$ is orthogonal. This completes the proof.

Proof. Let the $i$-th row of the orthogonal matrix $\boldsymbol{Q}$ be represented by a row vector $\boldsymbol{r}_i$. The product $\boldsymbol{Q}\boldsymbol{Q}^T$ would therefore be:

Since $\boldsymbol{Q}$ is orthogonal, we know that \eqref{eq:VGberAmNvO8jSBbFXKI} is equal to the identity matrix, which means that:

• the diagonal terms of \eqref{eq:VGberAmNvO8jSBbFXKI} must be $1$.

• the non-diagonal terms of \eqref{eq:VGberAmNvO8jSBbFXKI} must be $0$.

Mathematically, we can write this as:

By theorem, the first equation can be written as:

Because magnitudes cannot be negative, we have that $\Vert\boldsymbol{r}_i\Vert=1$, that is, every row vector is an unit vector!

Next, since the dot product of $\boldsymbol{r}_i$ and $\boldsymbol{r}_j$ when $i\ne{j}$ is equal to zero, any pair of rows $\boldsymbol{r}_i$ and $\boldsymbol{r}_j$ are perpendicular to each other by definitionlink. This means that row vectors form an orthonormal setlink that spans $\mathbb{R}^n$, and thus the row vectors form an orthonormal basis of $\mathbb{R}^n$.

We now prove the converse, that is, if the row vectors of $\boldsymbol{Q}$ form an orthonormal basis of $\mathbb{R}^n$, then $\boldsymbol{Q}$ is orthogonal. The proof is very similar - let $\boldsymbol{Q}$ be defined as:

Where \eqref{eq:hrOax8UeTHrPQL7iQ6A} holds. $\boldsymbol{QQ}^T$ is:

Because $\boldsymbol{QQ}^T=\boldsymbol{I}_n$, we have that $\boldsymbol{Q}$ is orthogonal by definitionlink. This completes the proof.

Proof. The proof is nearly identical to that of theorem, except that we represent matrix $\boldsymbol{Q}$ using column vectors $\boldsymbol{c}_i$ instead of row vectors:

By definition of orthogonal matrices, we have that $\boldsymbol{Q}^T\boldsymbol{Q}=\boldsymbol{I}_n$. This means that:

The first equation implies $\Vert\boldsymbol{c}_i\Vert=1$, which means every column vector is an unit vector.

Next, by the definitionlink of dot product, every pair of $\boldsymbol{c}_i$ and $\boldsymbol{c}_j$ when $i\ne{j}$ must be orthogonal. This means that the column vectors of $\boldsymbol{Q}$ form an orthonormal set and spans $\mathbb{R}^n$. Therefore, the column vectors of $\boldsymbol{Q}$ form an orthonormal basis of $\mathbb{R}^n$.

We now prove the converse. Let $\boldsymbol{Q}$ be defined like so:

Where \eqref{eq:c5LLrknfeKg1oV66aEB} holds. Now, $\boldsymbol{Q}^T\boldsymbol{Q}$ is:

Because $\boldsymbol{Q}^T\boldsymbol{Q}=\boldsymbol{I}_n$, we have that $\boldsymbol{Q}$ is orthogonal by definitionlink. This completes the proof.

Proof. From the definition of orthogonal matrices, we know that:

Now, let's use the definition of orthogonal matrices once again to check if $\boldsymbol{Q}\boldsymbol{R}$ is orthogonal:

For the first step, we used the theoremlink $(\boldsymbol{A}\boldsymbol{B})^T=\boldsymbol{B}^T\boldsymbol{A}^T$. This completes the proof.

Proof. The matrix-vector product $\boldsymbol{Qx}$ results in a vector. By theoremlink, the magnitude of a vector can be written as a dot product like so:

To clarify the steps:

• the second equality uses theoremlink, that is, $\boldsymbol{A}\boldsymbol{v}\cdot\boldsymbol{w}= \boldsymbol{v}\cdot\boldsymbol{A}^T\boldsymbol{w}$.

• the second-to-last step uses theoremlink, that is, $\boldsymbol{x}\cdot\boldsymbol{x}= \Vert\boldsymbol{x}\Vert^2$.

This completes the proof.

Intuition. Recall that a matrix-vector product can be considered as a linear transformation applied to the vector. The fact that $\Vert\boldsymbol{Qx}\Vert=\boldsymbol{x}$ means that applying the transformation $\boldsymbol{Q}$ on $\boldsymbol{x}$ preserves the length of $\boldsymbol{x}$.

Proof. We know from this theoremlink that:

Where $\theta$ is the angle between $\boldsymbol{v}$ and $\boldsymbol{w}$. Similarly, we have that:

Where $\theta_*$ is the angle between $\boldsymbol{Qv}$ and $\boldsymbol{Qw}$. Our goal is to show that $\theta=\theta_*$.

We start by making $\theta_*$ in \eqref{eq:D7KabFz9nSld9XLbo08} the subject like so:

From theoremlink, we have that $\Vert{\boldsymbol{Qv}}\Vert=\Vert\boldsymbol{v}\Vert$ and $\Vert{\boldsymbol{Qw}}\Vert=\Vert\boldsymbol{w}\Vert$, thereby giving us:

We rewrite the dot product in the numerator as a matrix-matrix product:

Here, in the second step, we used theoremlink $(\boldsymbol{AB})^T=\boldsymbol{B}^T\boldsymbol{A}^T$. This completes the proof.

Solution. The vectors after the transformation are:

Let's visualize all the vectors:

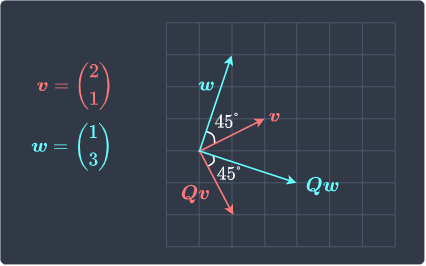
Observe the following:

• the length of the vectors remains unchanged after transformation.

• the angle between the two vectors also remains unchanged after transformation.

Proof. Recall from theoremlink that:

Since $\boldsymbol{Qx}$ and $\boldsymbol{Qy}$ are vectors, we can use \eqref{eq:bvWCKdz5Oa0Kj2YbNcl} to get:

We know from theoremlink that $\Vert\boldsymbol{Q}\boldsymbol{x}\Vert=\Vert{\boldsymbol{x}}\Vert$. Therefore, we have:

Using \eqref{eq:bvWCKdz5Oa0Kj2YbNcl} once more gives us the desired result:

This completes the proof.

Solution. By definition of orthogonal matrices, we have that:

Taking the determinant of both sides gives:

We know from theoremlink that the determinant of an identity matrix is $1$. Next, we know from theoremlink that $\det(\boldsymbol{AB})=\det(\boldsymbol{A})\cdot\det(\boldsymbol{B})$ for any two squares matrices $\boldsymbol{A}$ and $\boldsymbol{B}$. Therefore, \eqref{eq:OQGa4knzgaWQr3ShXuQ} becomes:

Next, theoremlink tells us that $\det(\boldsymbol{Q}^T)=\det(\boldsymbol{Q})$. Therefore, \eqref{eq:rm2ktxJUk80N1X6CTbx} becomes:

This completes the proof.

Matrices with orthogonal columns

Recall that the column vectors of an $n\times{n}$ orthogonal matrix form an orthonormal basis for $\mathbb{R}^n$. This means that:

• every column vector is an unit vector.

• every column vector is orthogonal to every other column vector.

In this section, we will look at a more relaxed version of an orthogonal matrix that only satisfies the second property.

Proof. Let $\boldsymbol{A}$ be an $n\times{n}$ matrix with orthogonal columns. The column vectors of $\boldsymbol{A}$ form an orthogonal basis of $\mathbb{R}^n$, which means that the set of column vectors is linearly independent by theoremlink. By theoremlink, $\boldsymbol{A}$ is invertible. This completes the proof.

Proof. Let $\boldsymbol{A}$ be an $n\times{n}$ matrix with orthogonal columns:

We can convert $\boldsymbol{A}$ into an orthogonal matrix $\boldsymbol{Q}$ by converting each column vector into a unit vector:

Here, the second equality holds by theoremlink.

By the propertylink of orthogonal matrices, we have that $\boldsymbol{Q}^T=\boldsymbol{Q}^{-1}$. Taking the transpose of both sides of \eqref{eq:BDLJ6XiStiRppatzIID} gives:

Where the second equality follows by theoremlink. The inverse $\boldsymbol{Q}^{-1}$ is:

Where the second equality holds by theoremlink. Equating $\boldsymbol{Q}^T= \boldsymbol{Q}^{-1}$ gives:

This completes the proof.

Proof. Since $\boldsymbol{A}$ has orthogonal columns, $\boldsymbol{A}$ is invertible by theoremlink. Because $\boldsymbol{A}$ is an upper triangular matrix, we have the following:

• $\boldsymbol{A}^{-1}$ is an upper triangular matrix by theoremlink.

• $\boldsymbol{A}^T$ is a lower triangular matrix by theoremlink.

Since $\boldsymbol{A}$ has orthogonal columns, $\boldsymbol{A}^{-1} =\boldsymbol{D}^2\boldsymbol{A}^T$ where $\boldsymbol{D}$ is some diagonal matrix by theoremlink. By theoremlink, $\boldsymbol{D}^2$ is also diagonal. Because $\boldsymbol{A}^T$ is a lower triangular matrix, the product $\boldsymbol{D}^2\boldsymbol{A}^T$ is also a lower triangular matrix by theoremlink. Because $\boldsymbol{A}^{-1}= \boldsymbol{D}^2\boldsymbol{A}^T$, we have that $\boldsymbol{A}^{-1}$ is a lower triangular matrix.

Therefore, $\boldsymbol{A}^{-1}$ is both upper triangular and lower triangular. The means that $\boldsymbol{A}^{-1}$ is a diagonal matrix. The inverse of a diagonal matrix is also diagonal by theoremlink, which means that $(\boldsymbol{A}^{-1})^{-1}=\boldsymbol{A}$ is also diagonal. This completes the proof.

Proof. By theoremlink, if $\boldsymbol{A}$ is an upper triangular orthogonal matrix, then $\boldsymbol{A}$ is a diagonal matrix. Suppose $\boldsymbol{A}$ is as follows:

Since $\boldsymbol{A}$ is orthogonal, the column vectors must be unit vectors. This means that the diagonal entries can either be $\pm1$ like so:

This completes the proof.