The absolute value of the determinant of a $2\times2$ matrix $\boldsymbol{A}$ is equal to the area of the parallelogram defined by the column vectors of $\boldsymbol{A}$. This is illustrated below:

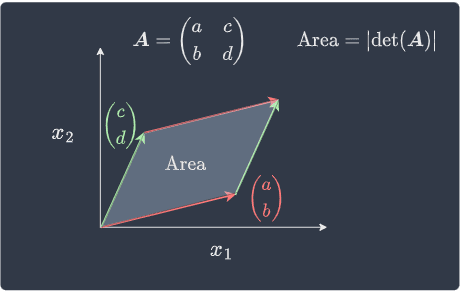
Proof. Suppose we have the following parallelogram identified by two vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ shown below:

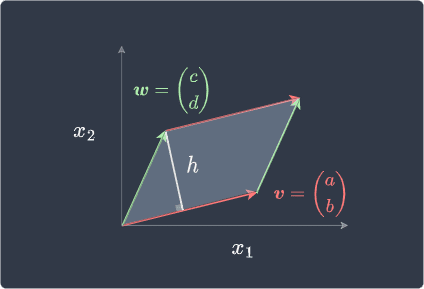
If we denote the height of the parallelogram as $h$ and the area of the parallelogram as $\mathrm{Area}$, then we know that:

$$\begin{equation}\label{eq:XFwRnApUtgx6L15fWyS} \mathrm{Area}=h\Vert{\boldsymbol{v}}\Vert \end{equation}$$

Where $\Vert{\boldsymbol{v}}\Vert$ is the length of $\boldsymbol{v}$. Now, we project the vector $\boldsymbol{w}$ onto the line $L$ spanned by vector $\boldsymbol{v}$, and denote the position vector of the projected point as $\mathrm{Proj}_L(\boldsymbol{w})$ like so:

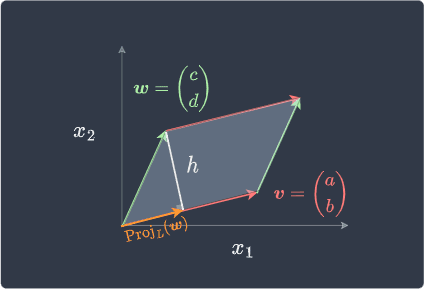
If you are unfamiliar with the concept of projections, please check out our guide on orthogonal projections first.

Using Pythagoras' theorem, we know that the following expression holds:

$$\begin{equation}\label{eq:nU1OFaU9ktZcpgXtEe9} h^2+\Vert\mathrm{Proj}_L(\boldsymbol{w})\Vert^2 =\Vert{\boldsymbol{w}}\Vert^2 \end{equation}$$

Now, recall from our guide on projections that:

$$\begin{equation}\label{eq:BskPkiRovQvZGn2away} \mathrm{Proj}_L(\boldsymbol{w})= \Big(\frac{\boldsymbol{w}\cdot\boldsymbol{v}} {\boldsymbol{v}\cdot{\boldsymbol{v}}}\Big) \boldsymbol{v} \end{equation}$$

Substituting \eqref{eq:BskPkiRovQvZGn2away} into \eqref{eq:nU1OFaU9ktZcpgXtEe9} gives:

$$\begin{equation}\label{eq:BSTvBmIzAJ2DtCzwkk7} \begin{aligned}[b] h^2+\Big\Vert\Big(\frac{\boldsymbol{w}\cdot\boldsymbol{v}} {\boldsymbol{v}\cdot{\boldsymbol{v}}}\Big) \boldsymbol{v}\Big\Vert^2 &=\Vert{\boldsymbol{w}}\Vert^2\\ h^2+\Big(\frac{\boldsymbol{w}\cdot\boldsymbol{v}} {\boldsymbol{v}\cdot{\boldsymbol{v}}}\Big) \boldsymbol{v}\cdot{ \Big(\frac{\boldsymbol{w}\cdot\boldsymbol{v}} {\boldsymbol{v}\cdot{\boldsymbol{v}}}\Big) \boldsymbol{v}} &=\Vert{\boldsymbol{w}}\Vert^2\\ h^2+\Big(\frac{\boldsymbol{w}\cdot\boldsymbol{v}} {\boldsymbol{v}\cdot{\boldsymbol{v}}}\Big) \Big(\frac{\boldsymbol{w}\cdot\boldsymbol{v}} {\boldsymbol{v}\cdot{\boldsymbol{v}}}\Big) (\boldsymbol{v}\cdot\boldsymbol{v}) &=\boldsymbol{w}\cdot{\boldsymbol{w}}\\ h^2+\Big(\frac{\boldsymbol{w}\cdot\boldsymbol{v}} {\boldsymbol{v}\cdot{\boldsymbol{v}}}\Big) (\boldsymbol{w}\cdot\boldsymbol{v}) &=\boldsymbol{w}\cdot{\boldsymbol{w}}\\ h^2+\frac{(\boldsymbol{w}\cdot\boldsymbol{v})^2} {\boldsymbol{v}\cdot{\boldsymbol{v}}} &=\boldsymbol{w}\cdot{\boldsymbol{w}} \end{aligned} \end{equation}$$

Now, to incorporate $\mathrm{Area}$ into equation \eqref{eq:BSTvBmIzAJ2DtCzwkk7}, we take the square of equation \eqref{eq:XFwRnApUtgx6L15fWyS} to get:

$$\begin{equation}\label{eq:MAPNdY431V49kANtAXr} \begin{aligned} (\mathrm{Area})^2&=h^2\Vert{\boldsymbol{v}}\Vert^2\\ &=h^2(\boldsymbol{v}\cdot{\boldsymbol{v}}) \end{aligned} \end{equation}$$

Making $h^2$ the subject and substituting this into equation \eqref{eq:BSTvBmIzAJ2DtCzwkk7} gives:

$$\begin{equation}\label{eq:I4ZiFmrsvgwE68LvIfZ} \begin{aligned}[b] \frac{(\mathrm{Area})^2}{\boldsymbol{v}\cdot{\boldsymbol{v}}}+\frac{(\boldsymbol{w}\cdot\boldsymbol{v})^2} {\boldsymbol{v}\cdot{\boldsymbol{v}}} &=\boldsymbol{w}\cdot{\boldsymbol{w}}\\ \frac{(\mathrm{Area})^2}{\boldsymbol{v}\cdot{\boldsymbol{v}}} &=\boldsymbol{w}\cdot{\boldsymbol{w}} -\frac{(\boldsymbol{w}\cdot\boldsymbol{v})^2}{\boldsymbol{v}\cdot{\boldsymbol{v}}}\\ (\mathrm{Area})^2&=(\boldsymbol{v}\cdot\boldsymbol{v}) (\boldsymbol{w}\cdot{\boldsymbol{w}}) -(\boldsymbol{w}\cdot\boldsymbol{v})^2\\ \end{aligned} \end{equation}$$

Now, suppose the components of $\boldsymbol{v}$ and $\boldsymbol{w}$ are:

$$\boldsymbol{v}= \begin{pmatrix}a\\b \end{pmatrix},\;\;\;\;\; \boldsymbol{w}= \begin{pmatrix}c\\d \end{pmatrix}$$

Given these components, let's simplify \eqref{eq:I4ZiFmrsvgwE68LvIfZ} to get:

$$\begin{equation}\label{eq:Cku06dVCDogexLVIscX} \begin{aligned}[b] (\mathrm{Area})^2&=(a^2+b^2)(c^2+d^2)-(ac+bd)^2\\ &=a^2c^2+a^2d^2+b^2c^2+b^2d^2-(a^2c^2+2acbd+b^2d^2)\\ &=a^2d^2+b^2c^2-2acbd\\ &=(ad-bc)^2 \end{aligned} \end{equation}$$

Now, let's define a matrix $\boldsymbol{A}$ whose columns are vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ like so:

$$\boldsymbol{A}=\begin{pmatrix} a&c\\ b&d\\ \end{pmatrix}$$

By theoremlink, we know that determinant of $\boldsymbol{A}$ is:

$$\begin{equation}\label{eq:B5meXlD1hVsmvXu6lqU} \mathrm{det}(\boldsymbol{A})=ad-bc \end{equation}$$

Substituting \eqref{eq:B5meXlD1hVsmvXu6lqU} into \eqref{eq:Cku06dVCDogexLVIscX} gives:

$$(\mathrm{Area})^2=\big(\mathrm{det}(\boldsymbol{A})\big)^2$$

Finally, taking the square root of both sides:

$$\mathrm{Area}=\vert\mathrm{det}(\boldsymbol{A})\vert$$

Here, since $\mathrm{det}(\boldsymbol{A})$ can be a negative number so we must take the absolute value when taking its square root. This completes the proof.

■

Example.

Finding the area of a parallelogram spanned by two vectors

Find the area of the parallelogram spanned by the following two vectors:

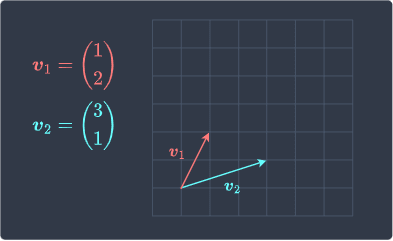
Solution. The parallelogram spanned by the two vectors is illustrated below:

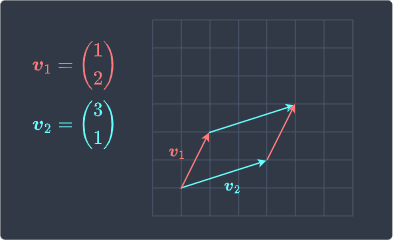
The matrix whose columns are the above vectors is:

$$\boldsymbol{A}= \begin{pmatrix} 1&3\\ 2&1 \end{pmatrix}$$

The area of the parallelogram is given by the absolute value of the determinant of $\boldsymbol{A}$ like so:

$$\begin{align*} \text{Area}&= \vert\det(\boldsymbol{A})\vert\\ &=\vert(1)(1)-(3)(2)\vert\\ &=\vert-5\vert\\ &=5\\ \end{align*}$$

Therefore, the area of the parallelogram is $5$.

■

The next theorem requires that you know matrix transformation can be considered a linear transformation.

Theorem.

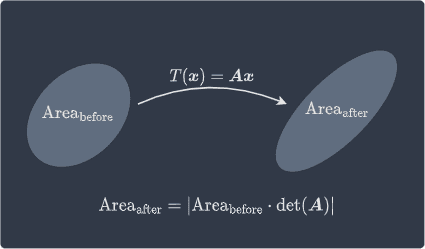
Determinant of a transformation matrix as a scaling factor of area/volume

The determinant of the transformation matrix $\boldsymbol{A}$ can be interpreted as the scaling factor of the area ($\mathbb{R}^2$ case) or the volume ($\mathbb{R}^3$ case):

Proof. We are going to prove this for a simple case in which the initial area is a rectangle. Note that this theorem works for all shapes.

Suppose we have the rectangle identified by two vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ below:

The area of the rectangle is simply:

$$\mathrm{Area}_{\mathrm{before}}=k_1k_2$$

We now define some transformation $T:\mathbb{R}^2\to\mathbb{R}^2$ like so:

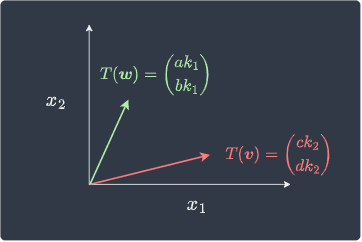
$$T(\boldsymbol{x})= \boldsymbol{A}\boldsymbol{x}= \begin{pmatrix} a&c\\ b&d\\ \end{pmatrix}\boldsymbol{x}$$

Let's apply our transformation matrix $\boldsymbol{A}$ on our vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ to get:

$$ \begin{align*} T(\boldsymbol{v})= \begin{pmatrix}ak_1\\bk_1\end{pmatrix}, \;\;\;\;\; T(\boldsymbol{w})= \begin{pmatrix}ck_2\\dk_2\end{pmatrix} \end{align*}$$

The transformed vectors $T(\boldsymbol{v})$ and $T(\boldsymbol{w})$ are shown below:

We can see that the area identified by the two vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ is now a parallelogram instead of a rectangle:

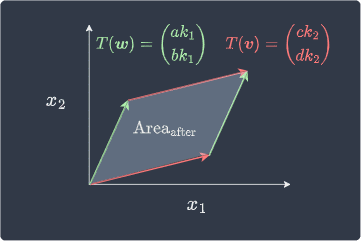
Our goal now is to derive an expression for $\mathrm{Area}_{\text{after}}$ in terms of $\mathrm{Area}_{\mathrm{before}}$.

Let $\boldsymbol{B}$ be a matrix whose columns are the transformed vectors of $\boldsymbol{v}$ and $\boldsymbol{w}$ like so:

$$\begin{align*} \boldsymbol{B}=\begin{pmatrix}ak_1&ck_2\\bk_1&dk_2\end{pmatrix} \end{align*}$$

We know from theoremlink that the determinant of $\boldsymbol{B}$ is equal to the area of the parallelogram:

$$\begin{align*} \mathrm{Area}_{\mathrm{after}} &=\vert\mathrm{det}(\boldsymbol{B})\vert\\ &=\vert{k_1k_2ad-k_1k_2bc}\vert\\ &=\vert{k_1k_2(ad-bc)}\vert\\ &=\vert{\mathrm{Area}_{\mathrm{before}}\cdot\mathrm{det}(\boldsymbol{A})}\vert \end{align*}$$

This means that the determinant of the transformation matrix $\boldsymbol{A}$ can be interpreted as a scaling factor of the transformed area!

■

Example.

Finding the area after transformation

Consider the rectangle spanned by the following two vectors:

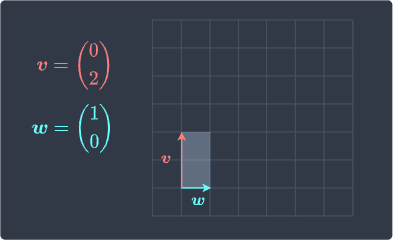
Suppose we apply the following transformation:

$$\boldsymbol{A}= \begin{pmatrix} 1&2\\2&1\\ \end{pmatrix}$$

What is the area of the parallelogram spanned by the transformed vectors?

Solution. The determinant of the transformation matrix can be interpreted as the scaling factor by which the area spanned changes after the transformation:

$$\text{Area}_\mathrm{after}= \vert\det(\boldsymbol{A})\cdot\text{Area}_\mathrm{before}\vert$$

The determinant of $\boldsymbol{A}$ is:

$$\begin{align*} \vert\det(\boldsymbol{A})\vert &=\vert(1)(1)-(2)(2)\vert\\ &=\vert-3\vert\\ &=3 \end{align*}$$

This means that the transformed area is $3$ times larger than the original area. The original area is simply a rectangle:

$$\text{Area}_{\mathrm{before}}=2$$

This means that the transformed area is $6$.

Let's now confirm this. The transformed vectors are:

$$\begin{align*} T(\boldsymbol{v})&=\boldsymbol{Av} \\&=\begin{pmatrix} 1&2\\2&1\\ \end{pmatrix} \begin{pmatrix} 0\\2\end{pmatrix}\\ &=\begin{pmatrix}4\\2\end{pmatrix}\\\\ T(\boldsymbol{w})&=\boldsymbol{Aw}\\&= \begin{pmatrix} 1&2\\2&1\\ \end{pmatrix} \begin{pmatrix} 1\\0\end{pmatrix}\\ &=\begin{pmatrix}1\\2\end{pmatrix} \end{align*}$$

The parallelogram spanned by these two vectors is:

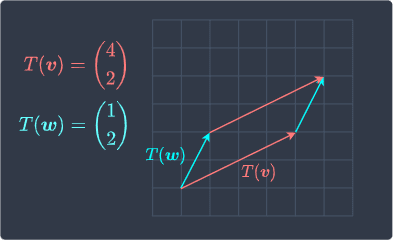
From visual inspection, it seems likely that the area of this parallelogram is $3$ times the area of the original rectangle. Let's still compute the area of the parallelogram using theoremlink - the area is equal to the determinant of the matrix whose columns are the transformed vectors:

$$\begin{vmatrix} 4&1\\2&2 \end{vmatrix}= (4)(2)-(1)(2)=6$$

Great, we've just shown that the transformed area is indeed $3$ times the original area!

■

Published by Isshin Inada

Edited by 0 others

Did you find this page useful?

thumb_up

thumb_down

Comment

Citation

Ask a question or leave a feedback...

thumb_up

thumb_down

chat_bubble_outline

settings

Enjoy our search

Hit / to insta-search docs and recipes!