Proof. The multiplication rule is simply a rearranged version of the formula of conditional probabilitylink:

This completes the proof.

Solution. Let's define the following events:

• event $\color{green}G_1$ - selecting a green ball for the first draw.

• event $\color{green}G_2$ - selecting a green ball for the second draw.

• event $\color{red}R_1$ - selecting a red ball for the first draw.

The probability of drawing $2$ green balls is:

The probability of drawing a red ball followed by a green ball is:

We've directly applied the formula for the multiplication rule of probability here, but we don't have to blindly apply the formula. We can approach this problem using a probability tree diagram as well:

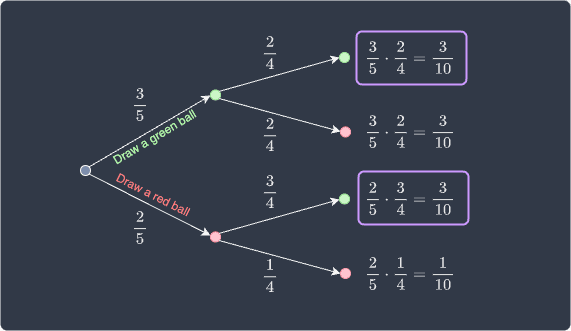
Here, the top bounded box is the probability of drawing two green balls and the bottom bounded box is the probability of drawing a red ball first followed by a green ball.

Proof. The multiplication rule for probabilities is:

If events $A$ and $B$ are independent, then this means that the probability of $A$ is not affected by the occurrence of $B$, which means that $\mathbb{P}(A\vert{B}) = \mathbb{P}(A)$. Therefore \eqref{eq:KNmyJfG7wjdt6LKwHg2} becomes:

This completes the proof.

Solution. Let $A$ and $B$ represent the outcome of the first and second dice respectively. The events $(A\text{ is even})$ and $(B\text{ is even})$ are independent because the outcome of the first dice does not affect the outcome of the second dice. Therefore, the probability that the outcomes of both dices are even is:

Proof. We can prove the addition rule by referring to the Venn diagram below:

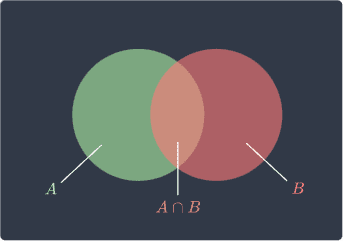
Let's start by confirming that the following is true:

Here, the $\setminus$ means exclusion. Taking the probability of both sides gives:

Since $A\setminus{B}$ and $B$ are disjoint, the third axiom of probabilitylink tells us that:

But $A\setminus{B}=A\setminus(A\cap{B})$ so that:

Now, refer to the Venn diagram again:

Confirm that the following is true:

Taking the probability of both sides gives:

Again, $A\setminus(A\cap{B})$ and $A\cap{B}$ are disjoint, and so by the third axiom of probability, we have that:

We rearrange this like so:

Finally, substituting \eqref{eq:PbZPnEWakXHqQISG5kU} into \eqref{eq:msEow9fqvJTNGWPgHqj} gives us the addition rule:

This completes the proof.

Solution. We define the following two events:

• event $A$ - outcome is even $\{2,4,6\}$.

• event $B$ - outcome is prime $\{2,3,5\}$.

Notice how rolling a $2$ satisfies both events, that is, $A\cap{B}=\{2\}$. Now, let's apply the addition rule:

Here, we must subtract by $\mathbb{P}(A\text{ and }B)$ because we are double counting the probability of getting a $2$.

Solution. We define the following two events:

• event $A$ - the drawn card is a hearts.

• event $B$ - the drawn card is red.

A standard deck contains $13$ hearts and $26$ red cards, of which half are hearts. Therefore, we are double counting all the hearts, which means that there are $13$ cards in the set $A\cap{B}$, that is, $\vert{A\cap{B}}\vert=13$. Let's apply the addition rule:

Proof. We know from the addition rule of probabilities that:

If $A$ and $B$ are two mutually exclusive events, then $\mathbb{P}(A\text{ and }B)=0$ because $A$ and $B$ can never occur together. Therefore, \eqref{eq:UOGUODp6B3g5DYYudoV} reduces down to:

This completes the proof.

Solution. Let's define the following events:

• event $A$ - rolling a $1$.

• event $B$ - rolling a $2$.

Clearly, these events are mutually exclusive because they cannot happen simultaneously, that is, we can never roll both a $1$ and a $2$ with a single roll. We now apply the addition rule for mutually exclusive events: