Solution. We can show the probability of every possible scenario using a probability tree diagram:

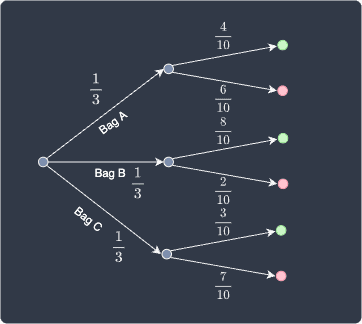
We define the following events:

• events $A$, $B$ and $C$ denote choosing bags $A$, $B$ and $C$, respectively.

• events $\color{green}\text{green}$ and $\color{red}\text{red}$ denote choosing a green and red ball, respectively.

From the diagram, we can see that there are $3$ scenarios where we end up with a green ball:

• case 1 - we pick bag $A$, and then pick a green ball.

• case 2 - we pick bag $B$, and then pick a green ball.

• case 3 - we pick bag $C$, and then pick a green ball.

The probability that we draw a green ball is equal to the total sum of the probabilities that each of these cases would happen. The first case, for example, can be computed using the multiplication rulelink of probabilities:

Where $\mathbb{P}({\color{green}\text{green}}|A)$ is the probability that we select a green ball given that we selected bag $A$. Therefore, the probability of selecting a green ball is:

This answers the question but let's now dig deeper into the underlying theory, particularly how this relates to the partitioning of the sample space.

Partitioning of the sample space

The event that we draw a green ball can be illustrated as a Venn diagram:

Because there are $3$ possible ways in which a green ball is drawn (via bag $A$, $B$ or $C$), we can consider the following partitions:

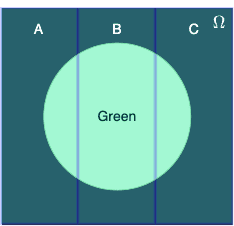
The event $A\cap\color{green}\mathrm{green}$ represents the intersection between partition $A$ and the green circle. In this context, the intersection symbol $\cap$ is to be interpreted as "and". Notice how we obtain the entire green circle by taking the union of all the intersections of each partition and the green circle, that is:

Note the following:

• $\mathbb{P}(A)+ \mathbb{P}(B)+ \mathbb{P}(C)=1$, that is, the probabilities of randomly selecting a bag add up to one. When this is true, we say that the partitions $A$, $B$ and $C$ constitute a sample space.

• the partitions do not necessarily have to be equally sized. In this case though, the partitions are of equal size since $\mathbb{P}(A) =\mathbb{P}(B) =\mathbb{P}(C)=1/3$.

Taking the probability of both sides of \eqref{eq:BHCuIgBSvU5xYYGmXEF} gives:

Notice how three events $(A\cap{\color{green}\text{green}})$, $(B\cap{\color{green}\text{green}})$ and $(C\cap{\color{green}\text{green}})$ are mutually exclusive because they cannot happen simultaneously. Therefore, the third axiom of probabilitylink tells us that:

Now, recall the multiplication rule of probabilities, which is simply a rearranged version of the formula of conditional probability:

Where:

• $E_1$ and $E_2$ are some events.

• $\mathbb{P}(E_2\vert{E_1})$ is the probability of $E_2$ occurring given $E_1$ has occurred.

Applying this rule to \eqref{eq:dGnNFcZT5VuRfit3btu} gives:

This is exactly the same formula \eqref{eq:xfN7kxAYwCrmDjDInlD} we used earlier! This formula is called the law of total probability.

Proof. The flow of the proof is very similar to how we solved the example problem earlier. Suppose events $B_1$, $B_2$, $\cdots$, $B_k$ constitute a partition of the sample space $S$, that is:

For instance, for $k=5$, the Venn diagram may look like the following:

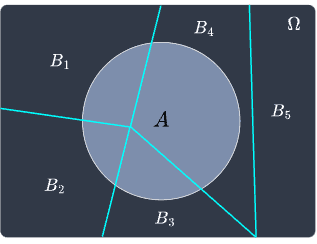
Notice how not all partitions need to intersect with event $A$. Now, event $A$ can be constructed by summing up all the intersection between $A$ and the partitions $B_1$, $B_2$, $\cdots$, $B_k$, that is:

Taking the probability of both sides yields:

Because the events $(B_i\cap{A})$ where $i=1$, $2$, $\cdots$, $k$ are disjoint, the third axiom of probabilitylink tells us that:

Using the multiplication rule, that is $\mathbb{P}(B\cap{A}) =\mathbb{P}(B) \cdot\mathbb{P}(A|B)$, we have the following:

This completes the proof.

As a reference for the latter guides, we will also state the law of total probability when there are only two events $B_1$ and $B_2$ that partition the sample space.